2024. 7. 27. 00:08ㆍ코딩 테스트(JAVA)/리트코드
37. Sudoku Solver
문제
https://leetcode.com/problems/sudoku-solver/description/

Example 1:
Input:
board = [["5","3",".",".","7",".",".",".","."],
["6",".",".","1","9","5",".",".","."],
[".","9","8",".",".",".",".","6","."],
["8",".",".",".","6",".",".",".","3"],
["4",".",".","8",".","3",".",".","1"],
["7",".",".",".","2",".",".",".","6"],
[".","6",".",".",".",".","2","8","."],
[".",".",".","4","1","9",".",".","5"],
[".",".",".",".","8",".",".","7","9"]]
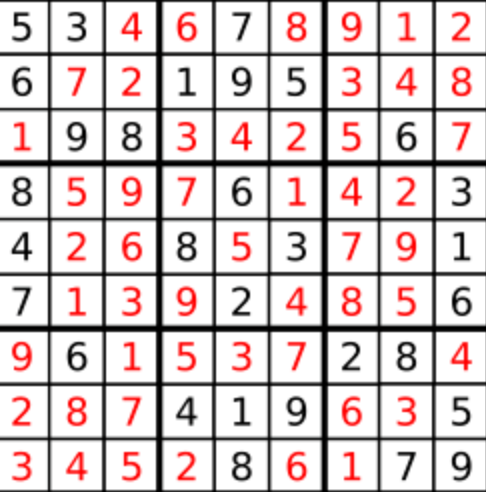
Output: [["5","3","4","6","7","8","9","1","2"],
["6","7","2","1","9","5","3","4","8"],
["1","9","8","3","4","2","5","6","7"],
["8","5","9","7","6","1","4","2","3"],
["4","2","6","8","5","3","7","9","1"],
["7","1","3","9","2","4","8","5","6"],
["9","6","1","5","3","7","2","8","4"],
["2","8","7","4","1","9","6","3","5"],
["3","4","5","2","8","6","1","7","9"]]
Constraints:
- board.length == 9
- board[i].length == 9
- board[i][j] is a digit or '.'.
- It is guaranteed that the input board has only one solution.
접근 방법
1. 어떤 알고리즘을 사용할까? 백트래킹
처음에는 완전탐색을 생각했다. 9*9를 기준으로 행과 열을 탐색하고 3*3안에서 중복되는 게 없는지 탐색하면 될 것 같았다. 하지만 이렇게 하면 시간복잡도가 9^81이라 시간초과가 난다. (각 칸마다 1부터 9까지 9가지 선택지 * 81번)
그럼 모든 경우의 수가 아닌 가능성 있는 것만 확인하는 백트래킹은 어떨까?
9*9로 사이즈가 고정되어 있고 가로, 세로, 3*3 확인을 + 총 81번 한다고 하면 9³ * 9² = 9⁵이다. 이는 10⁸ 안으로 들어가기에 백트래킹으로 풀어도 되겠다는 확신으로 코드 설계에 들어갔다.
2. 코드에 사용된 용어 설명
• s : 81개의 셀을 탐색
• (i, j) : 9*9에서의 셀 위치 계산 ➡ 맨 밑 [배우게 된 점]에서 자세한 설명
• isValid() :현재 숫자가 9*9 기준 행, 열, 그리고 3x3내에 중복되지 않는지 확인하는 메서드이다. 고정된 27개(가로, 세로, 작은 셀)를 확인하므로 시간복잡도는 O(1)이다. ➡ 맨 밑 [배우게 된 점]에서 자세한 설명
코드 구현
1. 실패 코드
public class SudokuSolver {
public void solveSudoku(char[][] board) {
backtracking(board, 0);
}
public boolean backtracking(char[][]board, int s){
if(s == 81) return true;
int i = s / 9;
int j = s % 9;
if(board[i][j] != '.'){
backtracking(board, s); // return문 없음 및 s+1로 수정
}
for(char c ='0'; c <= '9'; c++){ // c는 1부터 시작
if(isValid(board, i, j, c)){
board[i][j] = c;
backtracking(board, s+1);
board[i][j] = '.';
}
}
// 가능한 숫자가 없으면 false 반환
return true;
}
public boolean isValid(char[][]board, int row, int col, char c){
for(int i=0; i<9; i++){
if(board[i][col] == c || board[row][i] == c || board[3 * (row / 3) + i / 3 ][3 * (col / 3) + i % 3] == c){
return false;
}
}
return true;
}
}실패한 이유를 관련 코드에 주석으로 추가했다.
2. 실패 코드
public class SudokuSolver {
public void solveSudoku(char[][] board) {
backtracking(board, 0);
}
public boolean backtracking(char[][]board, int s){
if(s == 81) return true;
int i = s / 9;
int j = s % 9;
if(board[i][j] != '.'){
return backtracking(board, s+1);
}
for(char c ='1'; c <= '9'; c++){
if(isValid(board, i, j, c)){
board[i][j] = c;
// if-else로 묶기
if(backtracking(board, s+1)){
return true;
}
board[i][j] = '.';
}
}
return true;
}
public boolean isValid(char[][]board, int row, int col, char c){
for(int i=0; i<9; i++){
if(board[i][col] == c || board[row][i] == c || board[3 * (row / 3) + i / 3 ][3 * (col / 3) + i % 3] == c){
return false;
}
}
return true;
}
}실패한 이유를 관련 코드에 주석으로 추가했다.
3. 성공 코드
public class SudokuSolver {
public void solveSudoku(char[][] board) {
backtracking(board, 0);
}
public boolean backtracking(char[][] board, int s) {
// 만약 s가 81이면 모든 셀을 확인했으므로 true 반환
if (s == 81) return true;
// (i, j): s를 통해 9*9에서의 셀 위치 계산
int i = s / 9;
int j = s % 9;
// 현재 셀이 빈 셀이 아니면 다음 셀로 이동
if (board[i][j] != '.') {
return backtracking(board, s + 1);
}
for (char c = '1'; c <= '9'; c++) {
// 현재 셀에 숫자 c를 넣을 수 있는지 확인
if (isValid(board, i, j, c)) {
// 숫자 c를 현재 셀에 넣음
board[i][j] = c;
// 다음 셀로 이동하여 백트래킹 호출
if (backtracking(board, s + 1)) {
// 성공적으로 해결된 경우 true 반환하여 현재 함수를 종료하고 이전 호출 스택으로 돌아감
return true;
} else {
// 현재 숫자가 정답이 아니라면 해당 셀 초기화
board[i][j] = '.';
}
}
}
// 모든 숫자를 시도해도 해결되지 않은 경우 false 반환
return false;
}
public boolean isValid(char[][] board, int row, int col, char c) {
// 현재 숫자 c가 행, 열, 3x3 박스 내에 중복되지 않는지 확인
for (int i = 0; i < 9; i++) {
// 행을 기준으로 중복 확인
if (board[i][col] == c) return false;
// 열을 기준으로 중복 확인
if (board[row][i] == c) return false;
// 3x3 박스를 기준으로 중복 확인
if (board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] == c) return false;
}
return true;
}
}• 실행 시간 (Runtime): 9ms
• 메모리 사용량 (Memory): 40.90MB
배우게 된 점
1. i와 j를 통해 현재 row와 col을 알 수 있다.
int i = s / 9;
int j = s % 9;
[예]
s:17 -> (1,8)
9*9 격자내의 17번째 셀의 위치는 (1,8)이다.
2. 9*9 격자 및 3x3 작은 격자 내의 각각의 셀에 접근하기 위한 수식
(row / 3)와 (col / 3)
: 현재 셀이 속한, 3*3 격자의 행과 열을 나타낸다.
3 * (row / 3)와 3 * (col / 3)
3을 곱하는 이유는 3x3 격자의 시작 지점 셀로 이동하기 위함이다.
i / 3와 i % 3
3*3격자 내에서의, 9개의 셀 이동을 위해 하는 작업으로 각 격자의 행과 열을 나타낸다.
관련 코드
// 행을 기준으로 중복 확인
if (board[i][col] == c) return false;
// 열을 기준으로 중복 확인
if (board[row][i] == c) return false;
// 3x3 박스를 기준으로 중복 확인
if (board[3 * (row / 3) + i / 3][3 * (col / 3) + i % 3] == c) return false;
3. 재귀 함수 호출을 어디에 넣어야 할까? 한 번이 아닌 여러 번 호출 시 헷갈린다.
재귀 함수 호출은 그래프 탐색에서 다음 노드로 이동하는 것과 같기에 머릿속으로 트리, 그래프를 그려보고 언제 다음 노드로 이동해야 할지 생각해 보고 결정하면 조금 쉽다. 일반적으로 재귀함수는 베이스 케이스 → 현재 노드 방문 작업 → 다음 노드 방문 순으로 진행된다. 따라서 가장 마지막 부분에 재귀함수 호출부가 오는 경우가 많다.
'코딩 테스트(JAVA) > 리트코드' 카테고리의 다른 글
| [리트코드] 51. N-Queens (0) | 2024.07.29 |
|---|---|
| [리트코드] 131. Palindrome Partitioning 회문 (0) | 2024.07.26 |
| [리트코드] 704. Binary Search - 반복분, 재귀 풀이 (0) | 2024.07.26 |
| [리트코드] 79. Word Search (0) | 2024.07.25 |
| [리트코드] 46. Permutations 순열, 77. Combinations 조합, 78. Subsets 부분집합 (1) | 2024.07.19 |