2024. 7. 29. 14:20ㆍ코딩 테스트(JAVA)/리트코드
51. N-Queens
문제
https://leetcode.com/problems/n-queens/description/

Example 1:
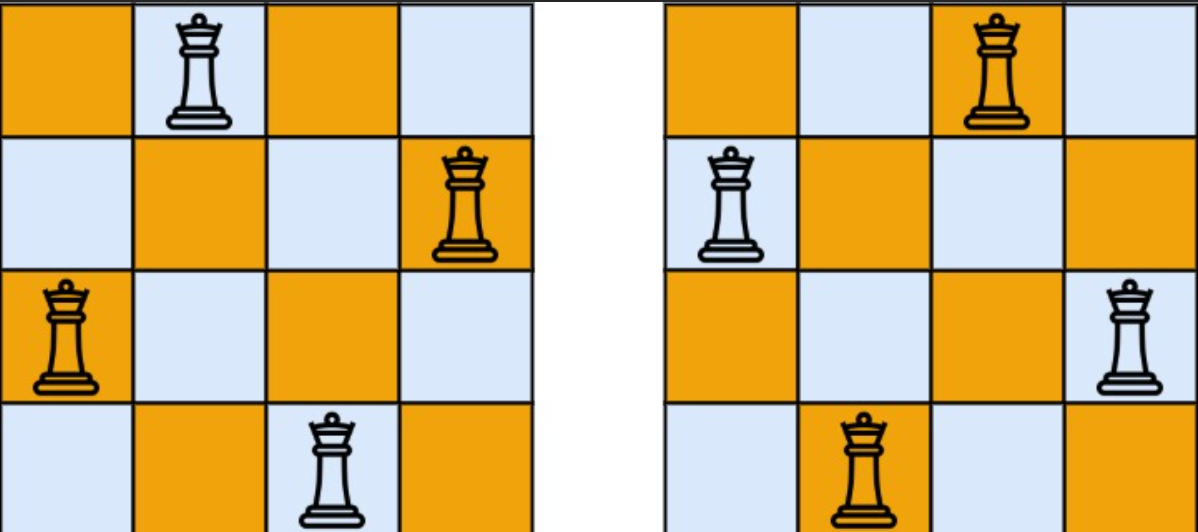
Input: n = 4
Output: [[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
Example 2:
Input: n = 1
Output: [["Q"]]
Constraints:
- 1 <= n <= 9
문제 분석
n * n 크기의 체스판에 n명의 여왕이 서로 공격할 수 없도록 위치시키는 문제로 퀸이 위치한 자리에서 같은 행, 열, 대각선에 다른 퀸이 없어야 한다.
• 'Q' : 여왕 위치
• '.' : 빈칸
입력
n : 여왕 수
출력
순서에 상관없이 가능한 모든 정답을 출력
접근 방법
아이디어 ➡️ 백트래킹
퀸은 같은 행, 열, 대각선에 다른 퀸이 위치할 수 없기 때문에 한 행에 한 퀸만 놓을 수 있다.
1. 검사하기:
각 방향당 최대 n번 검사: O(n)
4방향 검사 : 4 * O(n) = O(n)
2. 검사 횟수:
n개의 퀸을 놓아야 하므로 n번 검사
3. 체스판 경우의 수:
n개의 퀸을 n개의 행에 놓을 수 있는 모든 경우의 수 : n^n
따라서 최대 시간복잡도는 O(n * n * n^n) = O(n^n+2) = O(9^11) → 완전탐색으로는 시간초과가 나지만 백트래킹으로는 안쪽에 있을 것이라는 믿음으로 진행했다. (백트래킹은 정확한 시간복잡도를 구할 수 없다.)
코드 설계
1. 현재 위치(row, col)에서 상하좌우대각선을 이동할 수 있도록 상단 static 방향 변수 선언
2. 처음에는 board를 전부 '.'으로 채워두고 검사 진행 통과되면 'Q'로 수정
3. 만약 퀸을 배치한 행의 수와 체스판 길이가 같다면 answer에 넣어 반환
4. 현재 위치에 퀸을 놓을 수 있는지 판단하는 메서드에서 / 보드 경계 안에서만 반복문을 돌면서 (while), 다른 퀸과 충돌하지 않는지 그래서 퀸을 놓을 수 있는지 판별
코드 구현
고민 사항
backtracking 메서드의 반환값이 boolean이지만, 최종적으로는 모든 가능한 해를 answer에 추가해야 하는데 그럼 어떻게 해야 할까?
public class NQueens {
public List<List<String>> solveNQueens(int n) {
// 결과 리스트 생성
List<List<String>> answer = new ArrayList<>();
// 백트래킹 호출
backtracking(board, answer, n, 1);
return answer;
}
// 백트래킹
public boolean backtracking(List<List<String>> board, List<List<String>> answer, int n,
int row){
return false; // ???
}
}
backtracking 메서드의 반환값을 void로 변경하고 백트래킹 과정에서 해를 찾을 때마다 answer에 추가할 수 있도록 하자
// 백트래킹
public void backtracking(List<List<String>> board, List<List<String>> answer, int n,
int row){
if(row == n){
List<String> solutions = new ArrayList<>();
for(List<String> rows : board){
solutions.add(String.join("", rows));
answer.add(solutions); // 추가
}
}
...
}
1. 실패 코드
public class NQueens {
public List<List<String>> solveNQueens(int n) {
List<List<String>> board = new ArrayList<>();
for(int i=0; i<n; i++){
List<String> row = new ArrayList<>();
for(int j=0; j<n; j++){
row.add(String.valueOf('.'));
}
board.add(row);
}
List<List<String>> answer = new ArrayList<>();
backtracking(board, answer, n, 0);
return answer;
}
public static final int[] dx = {-1, -1, -1, 0, 1, 1, 1, 0};
public static final int[] dy = {-1, 0, 1, 1, 1, 0, -1, -1};
public void backtracking(List<List<String>> board, List<List<String>> answer, int n,
int row){
if(row == n){
List<String> solutions = new ArrayList<>();
for(List<String> rows : board){
solutions.add(String.join("", rows));
}
answer.add(solutions);
return;
}
for(int col = 0; col < board.size(); col++){
if(isValid(board, row, col)){
board.get(row).set(col, "Q");
backtracking(board, answer,n,row+1);
board.get(row).set(col, ".");
}
}
}
public boolean isValid(List<List<String>> board, int row, int col) {
for(int i=0; i<dx.length; i++){
int newRow = row;
int newCol = col;
while(newRow + dx[i] >= 0 && newRow + dx[i] <= board.size() && newCol + dy[i] <= board.size() && newCol + dy[i] >= 0) {
newRow += dx[i];
newCol += dy[i];
if(board.get(newRow).get(newCol).equals("Q")) {
return false;
}
}
}
return true;
}
}이유: board의 유효 범위 내에서 반복문을 실행해야 하는데, newRow + dx[i] <= board.size()의 경우 범위를 벗어난다. 왜냐하면 배열의 인덱스는 0부터 시작하기 때문에 board의 크기가 4라면 유효한 인덱스는 0부터 3까지이다.
2. 성공 코드
public class NQueens {
public List<List<String>> solveNQueens(int n) {
// 보드 생성 및 초기화
List<List<String>> board = new ArrayList<>();
for (int i = 0; i < n; i++) {
List<String> row = new ArrayList<>();
for (int j = 0; j < n; j++) {
row.add(String.valueOf('.')); /
}
board.add(row);
}
// 결과 리스트 생성
List<List<String>> answer = new ArrayList<>();
// 백트래킹 호출
backtracking(board, answer, n, 0);
return answer;
}
// 8방향 선언
public static final int[] dx = {-1, -1, -1, 0, 1, 1, 1, 0};
public static final int[] dy = {-1, 0, 1, 1, 1, 0, -1, -1};
// 백트래킹
public void backtracking(List<List<String>> board, List<List<String>> answer, int n, int row) {
// 현재 행과 n의 수가 같으면 모든 행에 퀸을 배치한 것이므로, 현재 보드 상태를 결과에 저장
if (row == n) {
List<String> solutions = new ArrayList<>();
for (List<String> rows : board) {
// 보드의 각 행을 ""로 구분하여 하나의 문자열로 합침
solutions.add(String.join("", rows));
}
answer.add(solutions);
return;
}
// 현재 행(row)에서 각 열(col)을 검사
for (int col = 0; col < board.size(); col++) {
if (isValid(board, row, col)) { // 현재 위치에 퀸을 놓을 수 있는지 검사
board.get(row).set(col, "Q"); // 퀸을 놓음
backtracking(board, answer, n, row + 1); // 다음 행으로 이동하여 재귀 호출
board.get(row).set(col, "."); // 퀸을 제거하여 원상태로 되돌림
}
}
}
// 현재 위치에 퀸을 놓을 수 있는지를 8방향에 대해 확인하는 메서드
public boolean isValid(List<List<String>> board, int row, int col) {
for (int i = 0; i < dx.length; i++) {
int newRow = row;
int newCol = col;
// 보드의 유효한 범위 내에서 반복문
while (newRow + dx[i] >= 0 && newRow + dx[i] < board.size() && newCol + dy[i] >= 0 && newCol + dy[i] < board.size()) {
newRow += dx[i];
newCol += dy[i];
// 현재 위치에 퀸이 있는지 확인, 퀸이 있으면 false 반환
if (board.get(newRow).get(newCol).equals("Q")) {
return false;
}
}
}
return true;
}
}• 실행 시간 (Runtime): 17ms
• 메모리 사용량 (Memory): 44.69MB
배우게 된 점
1. 2차원 배열에서 4방향 또는 8방향 이동을 나타내기 위한 방향 배열
주로 행렬이나 그리드에서 특정 좌표를 기준으로 상하좌우 및 대각선 방향으로 이동할 때 사용되는데 각각의 배열은 dx는 행 방향, dy는 열 방향을 나타낸다.
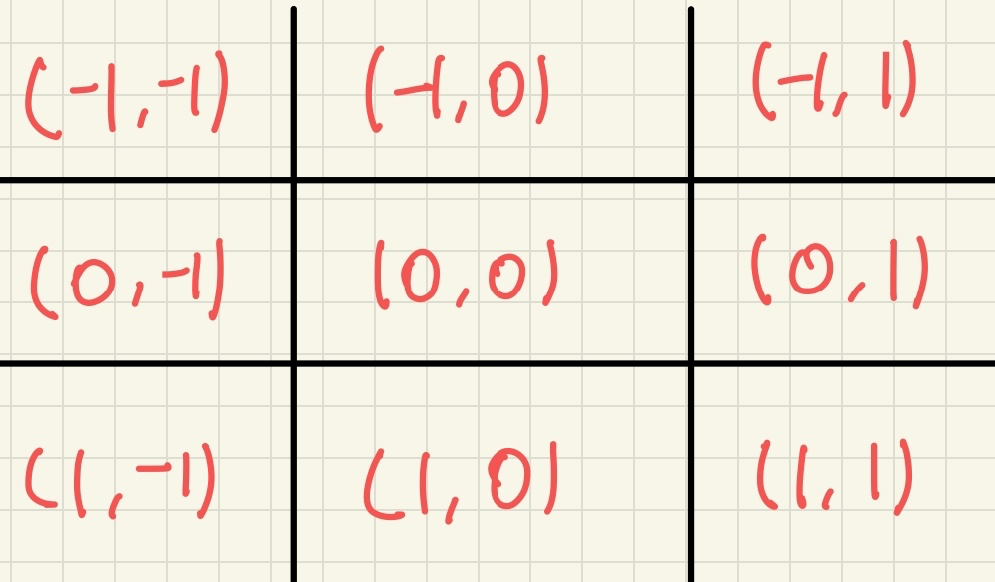
[8방향]
배열의 각 인덱스에 대응하는 값은 상좌, 상, 상우, 우, 하우, 하, 하좌, 좌이다. (시계방향)
private static final int[]dx= {-1, -1, -1, 0, 1, 1, 1, 0};
private static final int[]dy= {-1, 0, 1, 1, 1, 0, -1, -1};
[4방향]
배열의 각 인덱스에 대응하는 값은 상, 우, 하, 좌이다.
private static final int[] dx = {-1, 0, 1, 0};
private static final int[] dy = {0, 1, 0, -1};
2. String.valueOf()
문자열로 변환
3. String.join("", r)
r의 모든 요소를 빈 문자열("")로 구분하여 하나의 문자열로 합치는 방법이다.
예를 들어, r이 ["Q", ".", ".", "Q"]라면 String.join("", r)는 "Q..Q"를 반환한다.
'코딩 테스트(JAVA) > 리트코드' 카테고리의 다른 글
| [리트코드] 37. Sudoku Solver (0) | 2024.07.27 |
|---|---|
| [리트코드] 131. Palindrome Partitioning 회문 (0) | 2024.07.26 |
| [리트코드] 704. Binary Search - 반복분, 재귀 풀이 (0) | 2024.07.26 |
| [리트코드] 79. Word Search (0) | 2024.07.25 |
| [리트코드] 46. Permutations 순열, 77. Combinations 조합, 78. Subsets 부분집합 (1) | 2024.07.19 |